IEEE VIS 2024 Content: Revisiting Accurate Geometry for the Morse-Smale Complexes

Revisiting Accurate Geometry for the Morse-Smale Complexes

Son Le Thanh - KTH Royal Institute of Technology, Stockholm, Sweden

Michael Ankele - KTH Royal Institute of Technology, Stockholm, Sweden

Tino Weinkauf - KTH Royal Institute of Technology, Stockholm, Sweden

Download preprint PDF
Download camera-ready PDF

Room: Bayshore III

2024-10-14T16:00:00ZGMT-0600Change your timezone on the schedule page
2024-10-14T16:00:00Z
Exemplar figure, described by caption below
Shown is the Morse-Smale complex of an analytic function representing a circle engraved in a tilted plane. It can be computed using the provably correct steepest descent method as shown by the orange lines. This method struggles to produce a geometric embedding similar to that of continuous topology, i.e. the circular shape. Although several approaches have been proposed to address this issue, in this paper, we show systematically that they generate different topologies. We show that geometrical and topological accuracy can be achieved by applying the steepest descent method on a modified grid structure, illustrated by the white lines.
Abstract

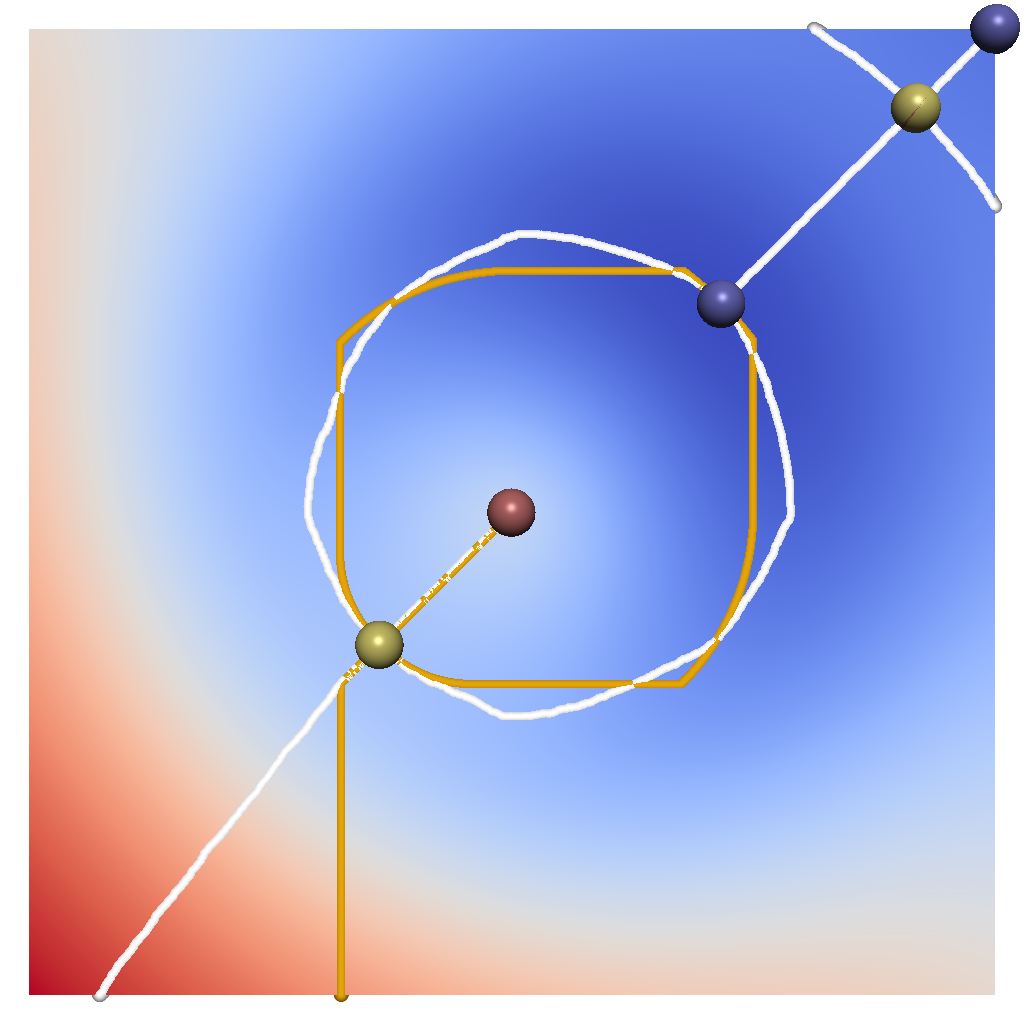
The Morse-Smale complex is a standard tool in visual data analysis. The classic definition is based on a continuous view of the gradient of a scalar function where its zeros are the critical points. These points are connected via gradient curves and surfaces emanating from saddle points, known as separatrices. In a discrete setting, the Morse-Smale complex is commonly extracted by constructing a combinatorial gradient assuming the steepest descent direction. Previous works have shown that this method results in a geometric embedding of the separatrices that can be fundamentally different from those in the continuous case. To achieve a similar embedding, different approaches for constructing a combinatorial gradient were proposed. In this paper, we show that these approaches generate a different topology, i.e., the connectivity between critical points changes. Additionally, we demonstrate that the steepest descent method can compute topologically and geometrically accurate Morse-Smale complexes when applied to certain types of grids. Based on these observations, we suggest a method to attain both geometric and topological accuracy for the Morse-Smale complex of data sampled on a uniform grid.